Как решать задачи с дробями?

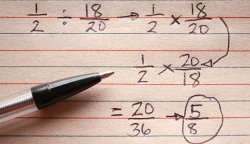
Ох уж эти дроби! В средней школе на математических уроках именно арифметические действия с дробями и задачи, где в условиях мелькают числа с числителями и знаменателями, становятся препятствием, которое многие школьники преодолевают с трудом. Запоминание и использование достаточно простых правил, которым подчиняются действия с дробями, для некоторых учеников становятся непреодолимым препятствие к хорошим оценкам по математике. Так как решать задачи с дробями? Это возможно, если понять правильно, что такое дробь.

Для наглядного примера возьмем обычный торт. Вы ожидаете гостей в количестве семи человек на праздник. Торт у вас один. Значит, поделить его необходимо на восьмерых (гости плюс именинник). Вы разрезали торт на равные части. Каждая из данных частей – это всего 1/8 от целого пирога. Вышла простая натуральная дробь, где 1 – это числитель, а 8 – знаменатель. Кто-то из гостей отказался от пирога, и вы решили взять себе еще один кусочек. Теперь вышло 2 куска от восьми частей пирога или 2/8.

Вдруг все ваши гости сидят на диетах, худеют и не желают есть торт? Тогда вам достается восемь частей из восьми (8/8), то есть, один целый торт!

Дроби, где числитель меньше знаменателя, называются правильными. А те, где больше числитель – неправильными.

Задачи с натуральными дробями
Задачи, в которых фигурируют натуральные дроби, чаще всего предполагают действия с ними. Самый легкий вариант такой задачи – это нахождение доли числа, которое выражено дробью. Вам вручили 6 килограмм яблок. 2/3 их них вы должны оставить на приготовление начинки для пирога. Умножаем 6 на 2, затем делим на 3. В результате имеем 4 кило, нужных для начинки.

Если стоит сложная задача найти число по его части, умножайте часть числа на дробь, поменяв местами числитель и знаменатель. Вот есть 6 килограмм яблок. Это 3/5 от общего количества яблок, собранных с вашей яблони. Значит, 6 умножаем быстро на 5 и делим на 3. Выходит 10 килограмм.

Как осуществляется деление и умножение дробей? Здесь правила просты. Умножая дробь на дробь, мы производим действия с числителями и знаменателями. Допустим, необходимо 2/3 умножить на 5/6. Число 2 умножаем на 5, а 3 умножаем на 6. Результат: 10/18. Если надо умножить дробь на целое число, просто перемножьте само число и числитель дроби. Так 3*4/7=12/7. Переводим дробь в правильную: 12/7=1 и 5/7.

Деление дробей легко заменяем умножением. Нужно разделить 5/6 на 2/3? Значит, первую дробь 5/6 оставляем неизменной, во второй меняем местами числитель и знаменатель. 5/6:2/3=5/6*3/2=15/12. Такие правила существуют и для деления натурального числа на дробь. 2:4/7= 2*7/4=14/4. Если дробь делим на натуральное число, то умножаем знаменатель и само число. 4/7:2=4/14.

Сложнее осуществить вычитание и сложение с дробями, где знаменатели разные. Если вам нужно прибавить к 3/8 дробь 2/8, тут проще. Складываете числители, оставляя знаменатели неизменными. Выходит 5/8. С вычитанием все так же, где от большего числителя отнимается меньший.

А как решить задачи с дробями, где разные знаменатели? Конечно, сначала привести их к одному. Нужно, допустим, сложить 5/8 и 2/3. Ищем методом подбора число, которое делится и на 8, и на 3. Это число 24. Чтобы из 5/8 сделать дробь со знаменателем 24, делим 24 на 8. Вышло число 3. Умножаем на 3 числитель. В итоге 5/8 равно 15/24. Также поступаем и с 2/3, получив 16/24. Далее можно складывать и вычитать знаменатели.

Получили неправильную дробь 31/24. 24/24 – это одно целое число. Вычтите из числителя знаменатель. Выходит 1 целая и 7/24.

Как быть, когда из целого числа нужно вычесть часть? У вас три торта, которые нужно разрезать на пять кусков каждый и отдать 2/5 кому-то знакомому. 3 – это 15, разделенное на пять. Значит, у вас 15/5 торта. Отнимите от 15 число 2, получится, что вам оставили 13/5 торта, или 2 целых и 3/5.

Вот так можно решать задачи с дробями. Главное, помните, что нельзя вычитать из меньшего числителя больший!