Навыки определения объема могут потребоваться в совершенно различных жизненных ситуациях. Например, когда вы отправляете груз транспортной компанией, то его важнейшими характеристиками, от которых зависит стоимость перевозки, будут являться его масса и объем. Если с массой все более или менее понятно, то определение объема заставит вас вспомнить некоторые свойства объемных фигур из школьного курса геометрии.
Подавляющее большинство коробок имеют форму прямоугольного параллелепипеда, в частных случаях превращающегося в куб. Объемом данной геометрической фигуры будет величина, которую занимает параллелепипед в трехмерном пространстве. Поэтому, объем коробки определяется следующим образом.
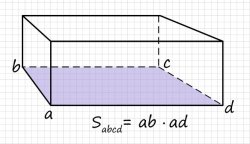
- В самом простом случае объем прямоугольного параллелепипеда, которым является коробка, равна произведению площади основания на высоту.
- Основанием прямоугольного параллелепипеда является плоская фигура прямоугольник, площадь которого, как известно равна произведению двух прилегающих к одному из прямых углов сторон. Основанием принято считать грань, которой фигура опирается на поверхность.
- После нахождения площади основания необходимо полученное значение умножить на высоту и таким образом будет определен объем коробки.
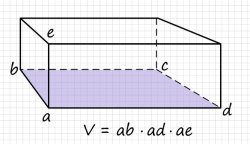
- Упрощенный алгоритм определения объема коробки таков. Вы должны выбрать любой угол коробки, измерить все три прилегающие к данному углу грани и перемножить их с соблюдением размерности. В результате перемножения вы получите размер коробки в кубических сантиметрах, или метрах, в зависимости от того, какие размерности вы использовали при перемножении.
- В частном случае, когда коробка представляет собой куб, то есть такой прямоугольный параллелепипед, у которого все грани равны, объем может быть вычислен возведением длины грани в третью степень.
Чтобы упростить вам задачу определения площади куба предлагаем вашему вниманию калькулятор, поставив в который значение трех прилегающих к одному углу граней, вы получите объем коробки.